Activation Functions : Sigmoid, tanh, ReLU, Leaky ReLU, and Softmax basics for Neural Networks and Deep Learning

Activation functions are mathematical functions that determine the output of a neuron and its output going to the next layer.The activation function does the non-linear transformation to the input making it capable to learn and perform more complex tasks.

Activation functions are an essential component of artificial neural networks, including deep learning models.

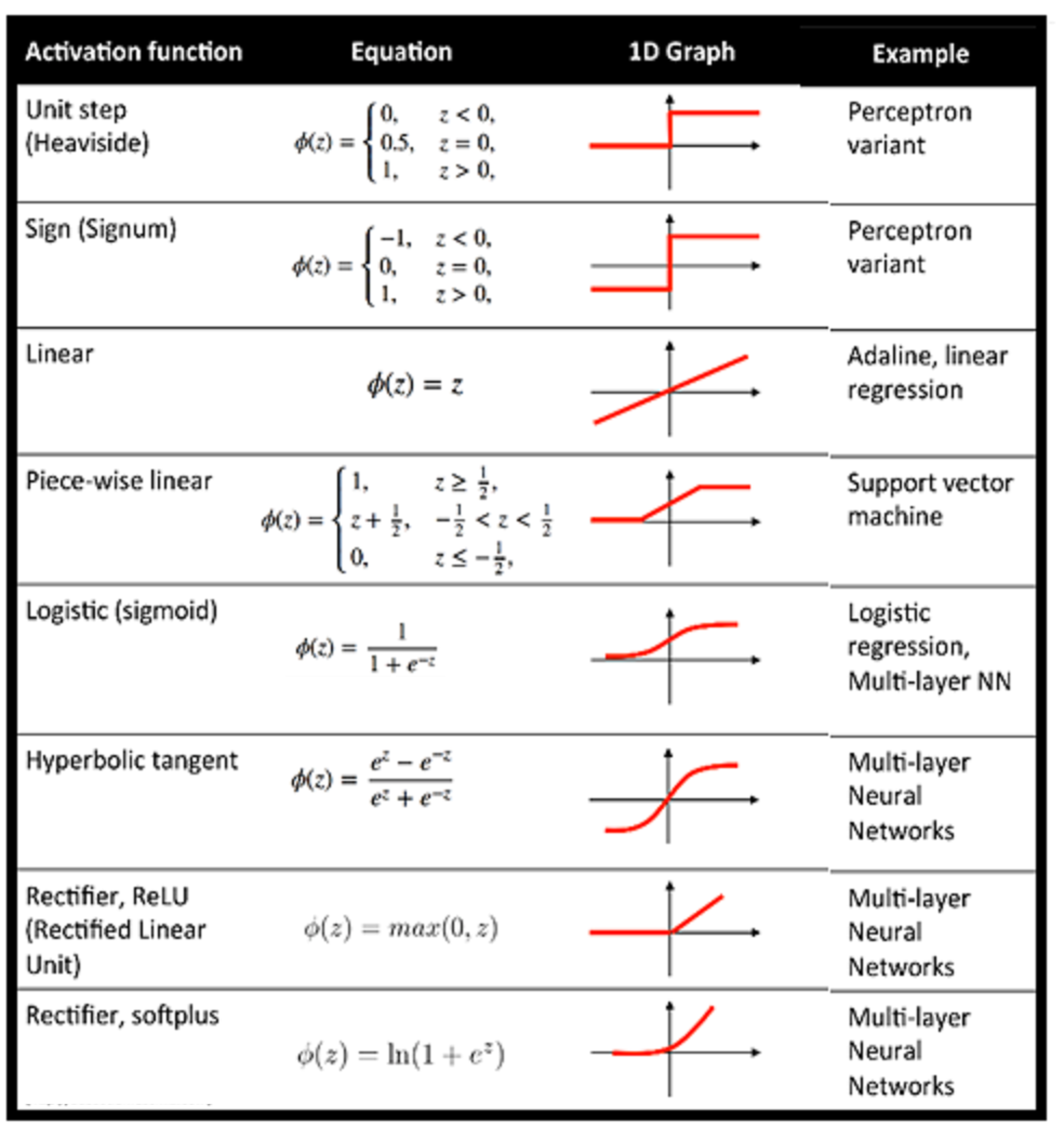
Here are some commonly used activation functions:

1. Step Function: It can be as simple as a step function that turns the neuron output on and off, depending on a rule or threshold. Or it can be a transformation that maps the input signals into output signals that are needed for the neural network to function.
2. Linear Activation Function: A linear activation function takes the form: A = cx It takes the inputs, multiplied by the weights for each neuron, and creates an output signal proportional to the input. In one sense, a linear function is better than a step function because it allows multiple outputs, not just yes and no.Linear activation function has two major problems:

   1. Not possible to use backpropagation (gradient descent) to train the model.

   2. All layers of the neural network collapse into one—with linear activation functions.

A neural network with a linear activation function is simply a linear regression model. It has limited power and ability to handle complexity varying parameters of input data.
3. Sigmoid activation function: The sigmoid activation function, also known as the logistic function, is a type of non-linear activation function commonly used in artificial neural networks. It maps the input value to a smooth and bounded output in the range of (0, 1), resembling an S-shaped curve.

   Vanishing gradient— for very high or very low values of X, there is almost no change to the prediction, causing a vanishing gradient problem. This can result in the network refusing to learn further, or being too slow to reach an accurate prediction.

4. Tanh (hyperbolic tangent) activation function: The tanh (hyperbolic tangent) activation function is a non-linear activation function commonly used in artificial neural networks. It maps the input value to a smooth and bounded output in the range of (-1, 1), similar to the sigmoid function.

The Tanh activation function is similar to the sigmoid function in shape but is centered at 0 and outputs negative values for negative inputs. It is symmetric around the origin, which means it has balanced positive and negative outputs. This property makes it suitable for certain types of neural networks, such as recurrent neural networks (RNNs), where capturing both positive and negative dependencies is essential.

5. Rectified Linear Unit (ReLU): The Rectified Linear Unit (ReLU) activation function is a non-linear activation function commonly used in artificial neural networks, particularly in deep learning architectures. It introduces non-linearity by mapping the input value to the maximum between the input and zero.

   The ReLU activation function is computationally efficient and avoids the vanishing gradient problem, which can occur in deep neural networks when gradients become too small during backpropagation. By allowing positive values to pass through unchanged, ReLU helps neural networks learn and represent complex non-linear relationships in the data.

   The Dying ReLU problem—when inputs approach zero, or are negative, the gradient of the function becomes zero, the network cannot perform backpropagation and cannot learn.